回溯

回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现，现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现。

TIP

回溯的本质是穷举。

理解递归

我看到有人说过一句话，不能理解回溯是因为没有理解递归。在别处看到了一个形象的例子：

递归最恰当的比喻，就是查词典。我们使用的词典，本身就是递归，为了解释一个词，需要使用更多的词。当你查一个词，发现这个词的解释中某个词仍然不懂，于是你开始查这第二个词，可惜，第二个词里仍然有不懂的词，于是查第三个词，这样查下去，直到有一个词的解释是你完全能看懂的，那么递归走到了尽头，然后你开始后退，逐个明白之前查过的每一个词，最终，你明白了最开始那个词的意思。

能用递归解决的问题都有这样一种特征：原问题可以分解为子问题，子问题和原问题的求解方法是一致的。最典型的递归的例子就是斐波那契数列的求解，假设我们需要求解第 5 位斐波那契数 F(5)，已知 F(0) = F(1) = 1：

• F(5) = F(4) + F(3)
• F(4) = F(3) + F(2)
• ......
• F(2) = F(1) + F(0)

F(1) + F(0) 就是这个子问题的尽头了，也就是递归的终止条件。

function fib(num) {
  if (num === 1 || num === 0) return 1;
  return fib(num - 1) + fib(num - 2);
}

console.log(fib(5)); // 8

由于动态规划和回溯中经常需要将大问题分解为小问题，因此经常需要使用递归的方法。

TIP

回溯是递归的副产品，只要有递归就会有回溯。

代码随想录 中总结了回溯的问题模板：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合问题

力扣链接：

• 77. 组合

• 216. 组合总和3

• 17. 电话号码的字母组合

  • 何时需要用 startIndex 何时不需要？
  • 如果是一个集合来求组合的话，就需要startIndex，例如：77.组合 (opens new window)，216.组合总和III (opens new window)。
  • 如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：17.电话号码的字母组合。

• 40. 组合总和2

  • 如何保证解集不包含重复的组合？参考代码回想录中的思路。
    • 树层去重的话，需要对数组排序。
    • 使用 used 数组，判断同一树层上元素（相同的元素）是否使用过。
    • 如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]，此时应该 continue。

切割问题

• 131. 切割字符串
  • 参考 代码随想录中的思路 ，体会切割问题和组合问题的不同。
• 91. 复原 IP 地址
  • 需要非常谨慎地处理各种条件中的等号问题。

子集问题

• 78. 子集
  • 组合和切割问题是找树的叶子节点，而子集问题是找树的所有节点。
  • 代码随想录 中强调：得到的结果是无序的，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始。
• 非递减子序列
  • 本题求子序列，很明显一个元素不能重复使用，所以需要 startIndex，调整下一层递归的起始位置。

通过全排列理解回溯

题目链接：力扣-全排列

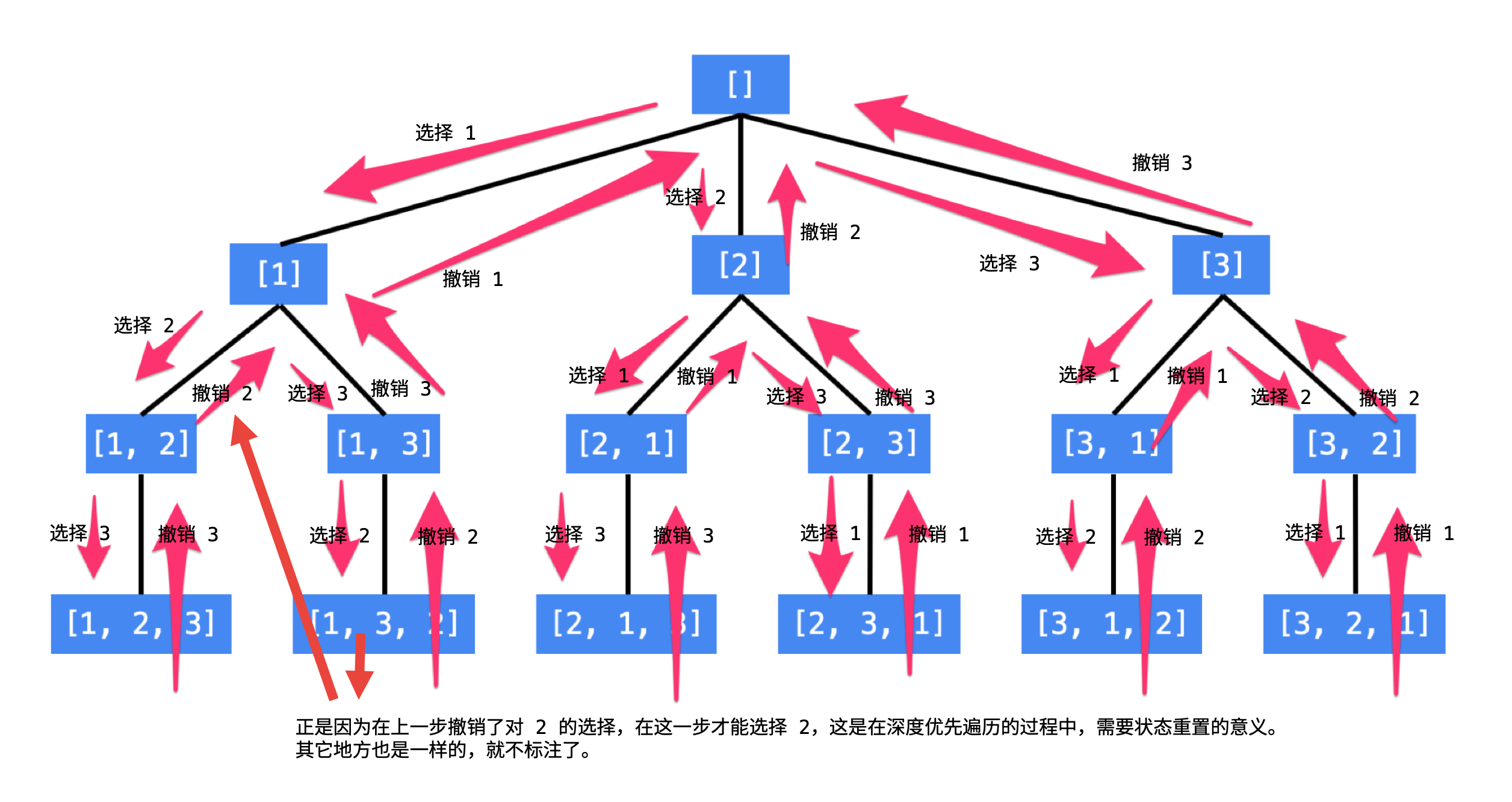
以例子中的 [1, 2, 3] 为例：

• 先写以 1 开头的全排列，它们是：[1, 2, 3], [1, 3, 2]，即 1 + [2, 3] 的全排列（注意：递归结构体现在这里）；
• 再写以 2 开头的全排列，它们是：[2, 1, 3], [2, 3, 1]，即 2 + [1, 3] 的全排列；
• 最后写以 3 开头的全排列，它们是：[3, 1, 2], [3, 2, 1]，即 3 + [1, 2] 的全排列。

按照这样的思路，就能画出一个树型结构：

参考

• 回溯法 - 维基百科，自由的百科全书
• Site Unreachable
• 代码随想录