和为k的子数组

最开始想用回溯去做：

var subarraySum = function (nums, k) {
  // 回溯
  let res = 0;

  function backtracking(startIndex, curSum) {
    if (curSum === k) {
      res += 1;
      return;
    }

    for (let i = startIndex; i < nums.length; i++) {
      curSum += nums[i];
      backtracking(i + 1, curSum);
      curSum -= nums[i];
    }
  }
  backtracking(0, 0);
  return res;
};

console.log(subarraySum([1, 2, 1], 2)); // 2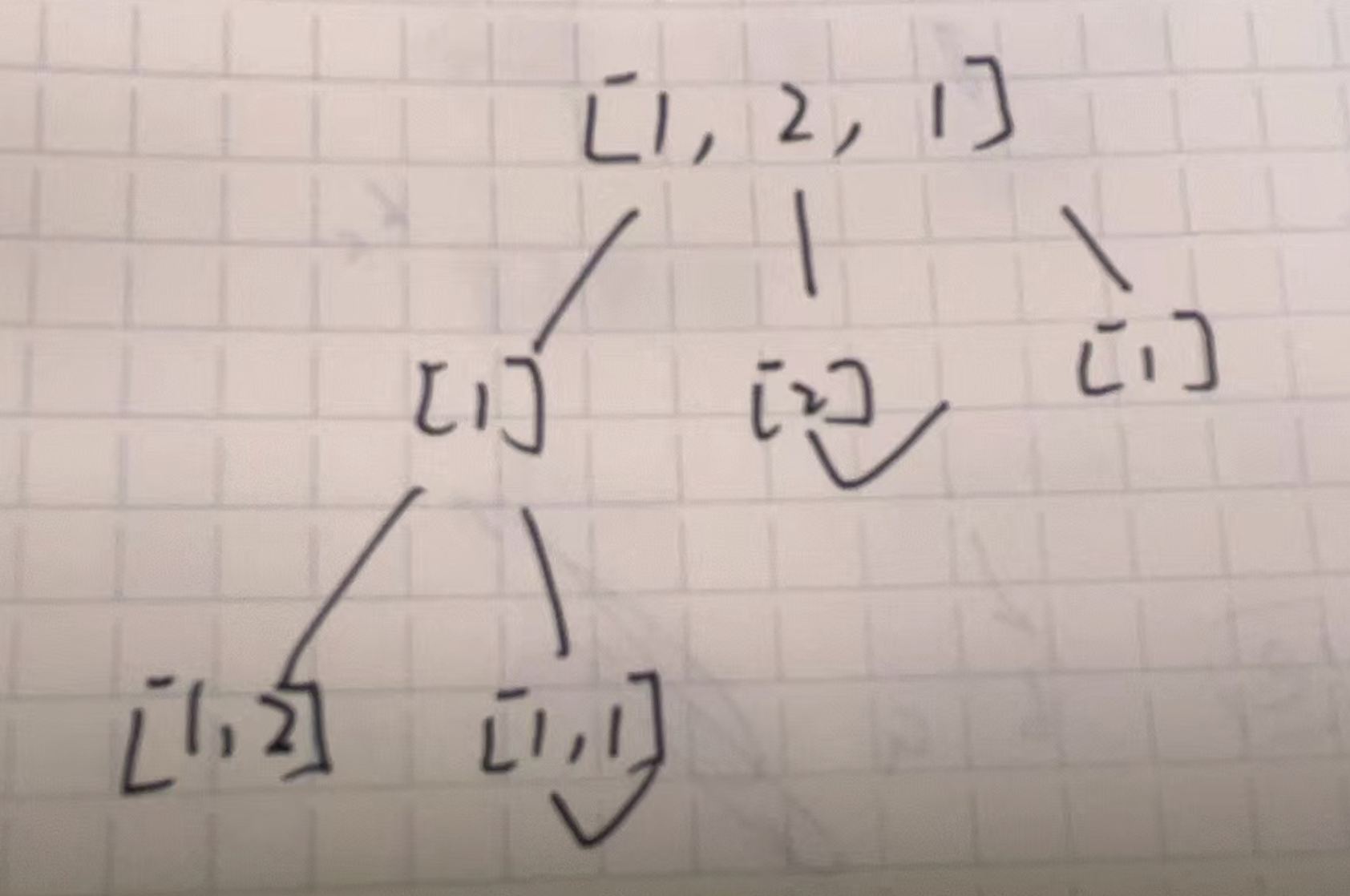

如图所示，上面这种方法将 [1, 1] 和 [2] 都算为一个答案，但这道题需要的是子数组、子序列，[1, 1] 中间是隔了一个元素的，不应该算在结果中，因此这种方法是存在问题的。

后面受到张张人的启发，想要使用滑动窗口的方法来解决问题：

var subarraySum = function (nums, k) {
  if(nums.length === 0) return 0;
  if(nums.length === 1) {
    if(nums[0] === k) return 1;
    return 0;
  }
  // 滑动窗口
  let l = 0, r = 0, res = 0;
  let curSum = nums[0];
  while (l < nums.length - 1) {
    if (curSum === k) {
      res += 1;
      l += 1;
      r += 1;
    } else if (curSum < k) {
      r += 1;
      curSum += nums[r];
    } else {
      curSum -= nums[l];
      l += 1;
    }
  }
  return res;
};

但是发现依然不行，因为数组中可能存在负数，比如 [-1, -1, 1] ，这种情况下右滑动整体不一定变大，左滑动整体也不一定减小，因此也无法使用滑动窗口的方法。😢

于是开始查看官方题解😛，有两个关键词：前缀和、哈希表。

前缀和可以简单理解为「数列的前 n 项的和」，是一种重要的预处理方式，能大大降低查询的时间复杂度 [^1]。

这里有一个技巧，利用前缀和快速计算数组区间和：

function calAllSum(nums) {
  // 前缀和数组
  const len = nums.length;
  const preSum = [0];
  for (let i = 0; i < len; i++) {
    preSum[i + 1] = nums[i] + preSum[i];
  }

  for (let l = 0; l < len; l++) {
    for (let r = l; r < len; r++) {
      console.log(
        `子数组 [${nums.slice(l, r + 1)}] 的区间和为 ${
          preSum[r + 1] - preSum[l]
        }`
      );
    }
  }
}
calAllSum([-1, -1, 1]);

输出为：

bash

子数组 [-1] 的区间和为 -1
子数组 [-1,-1] 的区间和为 -2
子数组 [-1,-1,1] 的区间和为 -1
子数组 [-1] 的区间和为 -1
子数组 [-1,1] 的区间和为 0
子数组 [1] 的区间和为 1

利用这一特性，就可以快速计算满足题目条件的子数组个数：

var subarraySum = function (nums, k) {
  // 计算前缀和数组
  const n = nums.length;
  const preSum = [0];
  nums.forEach((item, index) => {
    preSum[index + 1] = item + preSum[index];
  });
  console.log(preSum);

  let counts = 0;
  for (let l = 0; l < n; l++) {
    for (r = l; r < n; r++) {
      // 区间和 [l...r]
      if (preSum[r + 1] - preSum[l] === k) { 
        counts += 1;
      }
    }
  }
  return counts;
};

这种方法的时间复杂度为 $O (n^{2})$ ，还可以继续使用哈希表来优化：

var subarraySum = function (nums, k) {
  // 计算前缀和数组
  const n = nums.length;
  const preSum = [0];
  nums.forEach((item, index) => {
    preSum[index + 1] = item + preSum[index];
  });
  let counts = 0;
  const mp = new Map();
  for(let i = 0; i < preSum.length; i++) {
    const curSum = preSum[i];
    if(mp.has(curSum - k)) {
        counts += mp.get(curSum - k);
    }
    mp.set(curSum, (mp.get(curSum)|| 0) + 1);
  }
  return counts;
};

#todo 这种配合哈希表的方法还没有太懂，需要继续优化。

参考

[^1]: 前缀和 & 差分 - OI Wiki

和为k的子数组 ​

参考 ​

和为k的子数组

参考